Statistical Plots¶
A statistical plot (Stat plot on Factory’s interface) groups together 4 different types of plots, normally used to analyze correlation and dependencies present in the current dataset.
Differently from all the other plots offered by Rulex Platform, their graphical format is fixed by the definition itself of the statistical plot. Therefore, all the linked attributes are used only in a functional form, meaning that they affect the way points are evaluated, but not the chart’s graphical structure.
The statistical plots group contains the following types:
To select the plot type, users need to open the Plot option menu and select from the Statistic Plot Choice drop down menu the desired type. The default plot is Roc curve.
P-P plot¶
In statistics, a P-P plot (probability-probability plot or percent-percent plot or P value plot) is a probability plot, used to assess how closely a dataset fits a particular model.
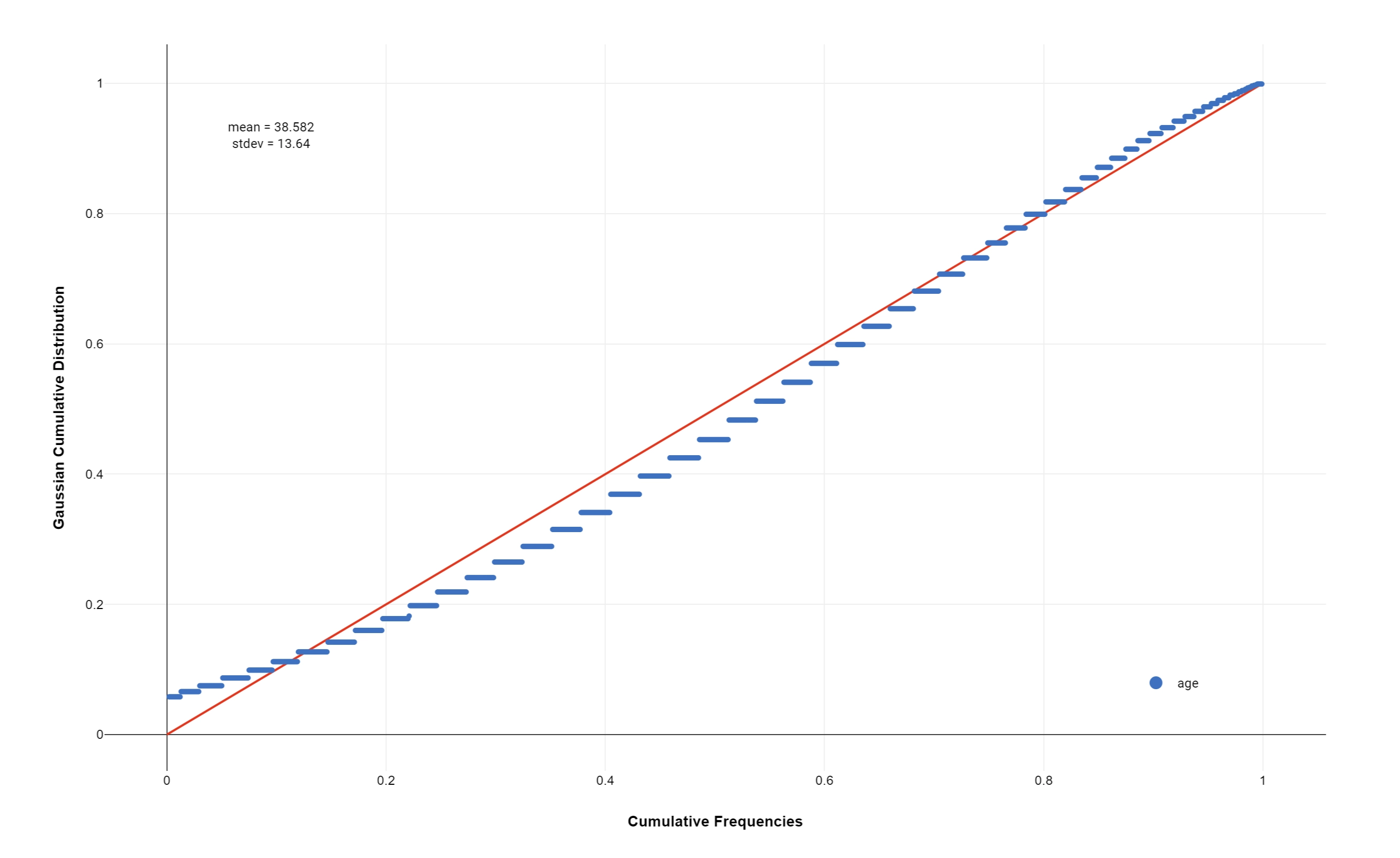
It works by plotting the two cumulative distribution functions against each other; if they are similar, the data will appear to be almost a straight line.
Dimension (mandatory fields are in bold) |
Type |
Description |
|---|---|---|
X |
feature |
It controls the variable used to evaluate the cumulative distribution function originating from data. |
The model used for the comparison is established in the Plot option menu through the following options:
Number of quantiles: the number of quantiles used to discretize the data and the model before evaluating the cumulative distributions.
- Compared distribution: the type of distribution to compare with the data. Available distributions are:
Normal
Exponential
Gamma
Beta
Cauchy
Logistic
Lognormal
Poisson
Note
Parameters of these distributions can be fixed from the same panel. If left blank, they are inferred from the data. The inferred value will be displayed as an annotation on the plot itself.
Q-Q plot¶
In statistics, a Q-Q plot (quantile-quantile plot) is a probability plot, a graphical method for comparing two probability distributions by plotting their quantiles against each other.
A point (x, y) on the plot corresponds to one of the quantiles of the second distribution (y-coordinate) plotted against the same quantile of the first distribution (x-coordinate).
This defines a parametric curve where the parameter is the index of the quantile interval.
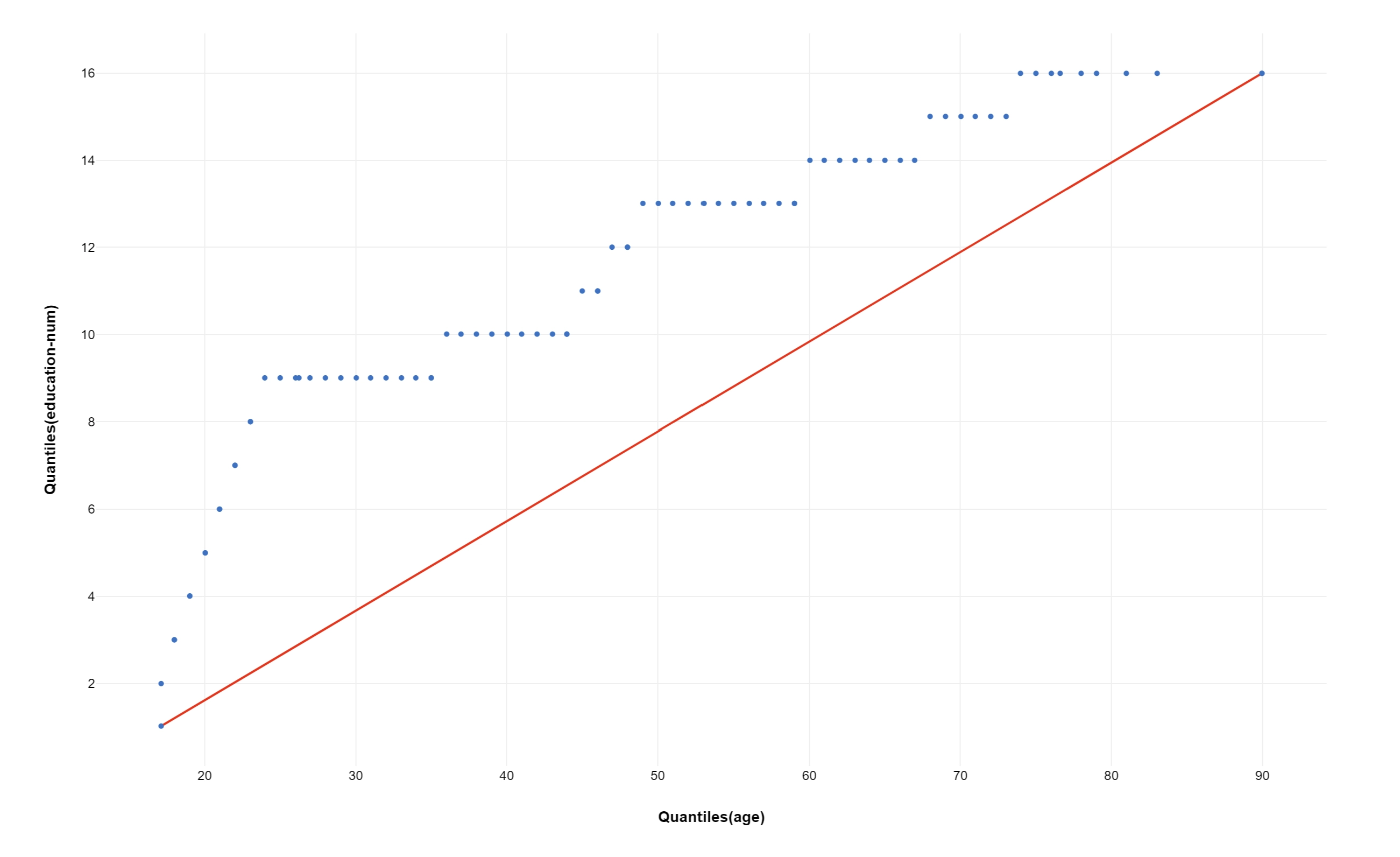
If the two compared distributions are similar, the points in the Q-Q plot will approximately lie on the identity line.
Dimension (mandatory fields are in bold) |
Type |
Description |
|---|---|---|
X |
feature |
It controls the variable used to evaluate the first probability distribution function originating from data. |
Y |
feature |
It controls the variable used to evaluate the second probability distribution function originating from data. |
Note
The attribute on the Y dimension is optional. If omitted, a model statistical distribution is used. The configuration of the model statistical distribution is performed in the same way as in the P-P plot.
Lorenz Curve¶
The Lorenz curve is a graphical representation of the Lorenz distribution, which is often associated with the distribution of wealth among the population, according to the Gini Index.
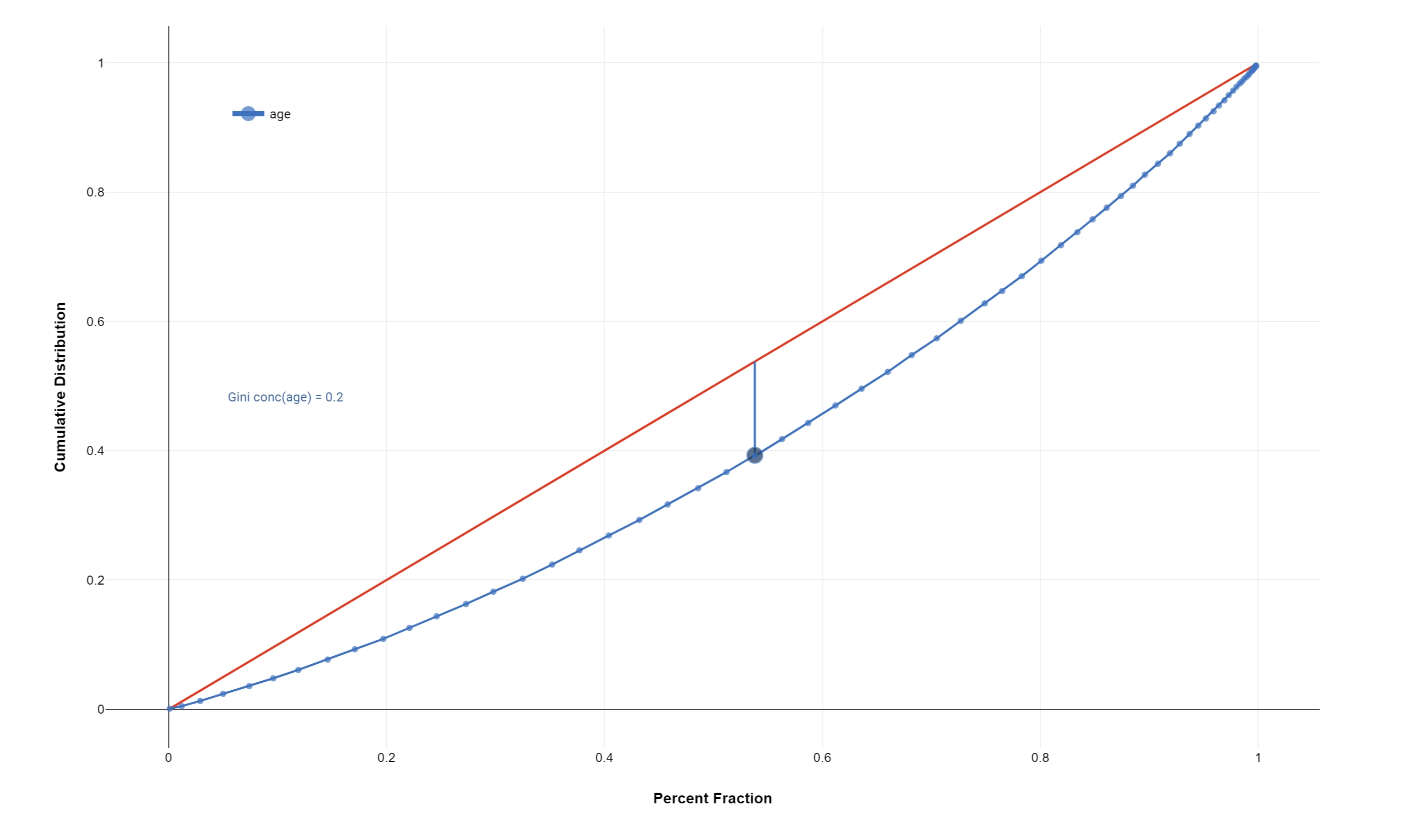
The more the curve sags below the straight diagonal line, the higher the degree of inequality of distribution.
Dimension (mandatory field are bold) |
Type |
Description |
|---|---|---|
X |
feature |
It controls the variable used to evaluate the Lorenz test. |
Note
Multiple attributes can be used on the X dimension, resulting in multiple Lorenz curves on the same plot.
ROC Curve¶
The ROC analysis is a useful tool to evaluate the performance of tests and, more generally, to evaluate the accuracy of a statistical model (i.e. logistic regression, linear discriminant analysis) classifying subjects into different categories.
A ROC Curve is a plot of sensitivity on the y-axis against (1−specificity) on the x-axis for varying values of the threshold t. The 45° diagonal line connecting (0,0) to (1,1) is the ROC curve corresponding to random chance. The ROC Curve for the gold standard is the line connecting (0,0) to (0,1) and (0,1) to (1,1). Generally, ROC curves lie between these 2 extremes.
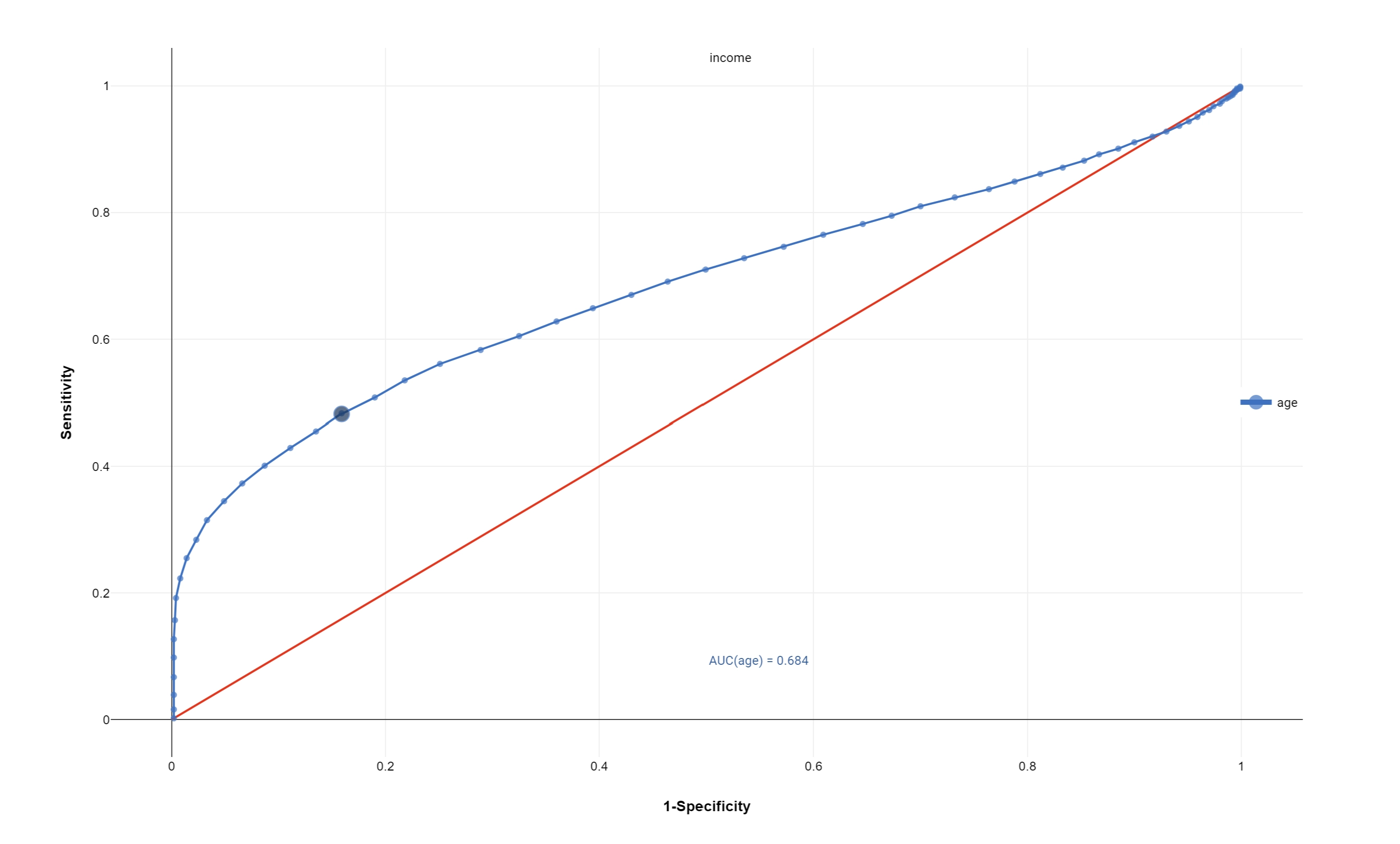
The area under the ROC curve is a summary measure that consists of the diagnostic average of the accuracy across the spectrum of test values.
Dimension (mandatory fields are in bold) |
Type |
Description |
|---|---|---|
X |
feature |
It controls the variables used to evaluate the Lorenz test. |
Target |
target |
It is used as the classifier output for the test, defining the final classes of the hypothetical classification. |
Note
Multiple attributes can be used on the X dimension, resulting in multiple ROC Curves on the same plot. The name of the single used target is highlighted in the default title of the ROC plot.
Users can customize the ROC analysis by configuring the range of values which leads to a Positive test. This can be done through a dedicated option in the Plot option menu. Available values are:
Lower values (default)
Greater values
Automatic selection